Teorema de Pitágoras
Teorema de Pitágoras
Si se tiene un triángulo rectángulo de lados a, b y c, siendo a y b los catetos, es decir, los lados que forman un ángulo recto. La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.

En otras palabras, si a un triángulo rectángulo, le trazas un cuadrado en cada uno de sus lados, siendo este lado, la medida del lado del cuadrado, y obtienes el área de cada uno de ellos; el área del cuadrado de la hipotenusa, que es el lado mayor, es igual a la suma de las áreas de los cuadrados de los catetos, que son los lados menores que forman el ángulo recto.
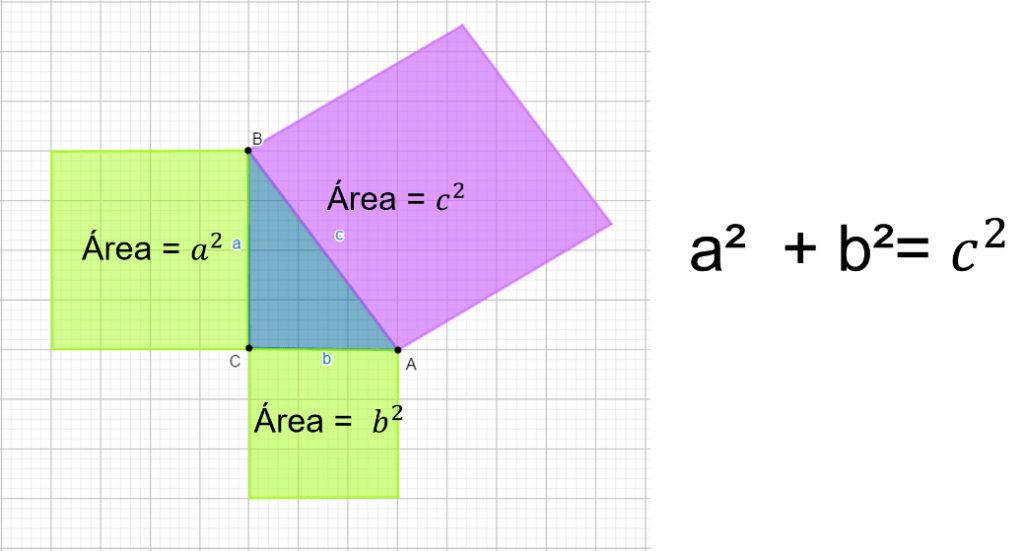
Observa el siguiente ejemplo obtenido de un libro de texto de Matemáticas de tercero.
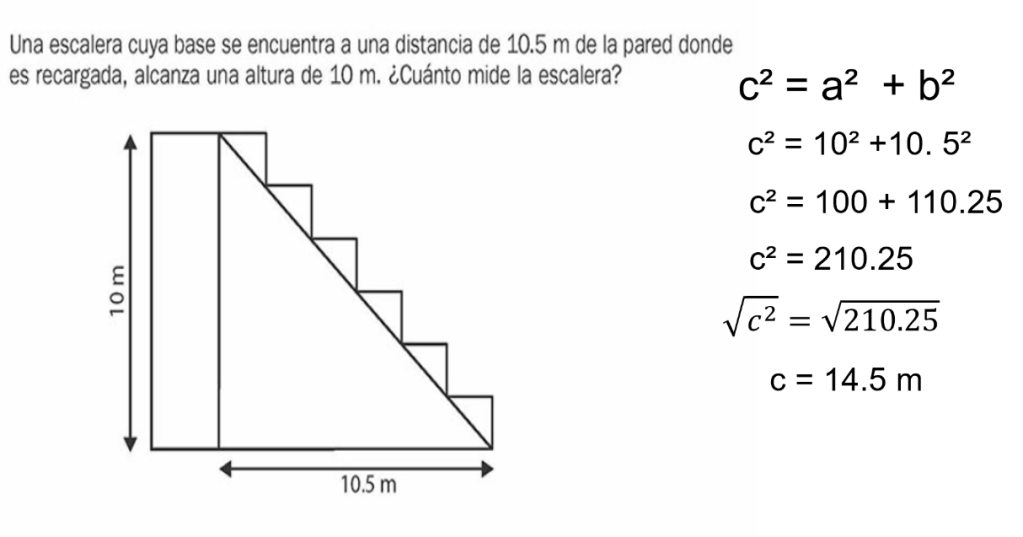
Ejercicios
1 En la esquina de una plaza rectangular se encuentra un puesto de helados. Si estoy en la esquina opuesta diagonalmente,
¿Cuántos metros tengo que recorrer en diagonal para llegar al puesto? Los lados de la plaza miden 48 m y 64 m.
2 Hallar el área de la región sombreada de la siguiente figura:

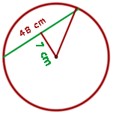
3 En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
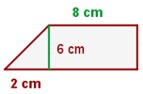
4 Hallar el perímetro y el área del trapecio rectángulo:
Respuestas
Ecuaciones Cuadráticas (Fórm. Gral.)
La forma estándar de la ecuación de segundo grado es la siguiente:
En donde: "a" es el termino cuadrático, "b" es el termino lineal y "c" es el termino independiente.
Antes de resolver una ecuación usando la fórmula cuadrática, es vital estar seguros de que
la ecuación tenga esta forma. Si no, podríamos usar los valores incorrectos de a, b, o c y la fórmula
dará soluciones incorrectas.
La formula general para encontrar la solución de una ecuación de segundo grado es:
Para resolver una ecuación utilizanda la formula general podemos realizar los siguientes pasos
- Pon primero la ecuación en su forma estándar.
- Identifica los coeficientes, a, b y c. Ten cuidado de incluir los signos negativos si los términos b o c se restan.
- Sustituye los valores por los coeficientes en la fórmula cuadrática.
- Simplifica lo más posible.
- Usa el ± en frente del radical para separar la solución en dos valore: uno en el que la raíz cuadrada se suma y el otro en el que la raíz cuadrada se resta.
- Simplifica ambos valores para obtener las posibles soluciones.
Ejemplo: usa la formula cuadrática para resolver la ecuacion.
Ejercicios
1 Resuelve la siguiente ecuación:
2 José Luis es tres años mayor que su hermano Jesús. Si la suma de los cuadrados de sus edades es 369.
¿Cuántos años tiene José Luis?
3 Resuelve la siguiente ecuación.
4 Encuentra un número que elevado al cuadrado y disminuido el doble de dicho número da como resultado siete veces el número sumado a 10.
Respuestas
Volumen de cilindros y conos
El cilindro consta de dos bases circulares y una cara curva que los une.
El cono tiene una base circular y una cara curva que termina en el extremo opuesto a la base, en un vértice.
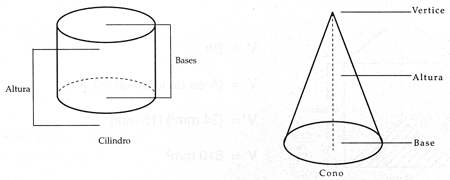
Cilindros
Para conocer el volumen de un cilindro se multiplica el área de la base por su altura, o sea:
Donde B se obtendrá con la fórmula para calcular el área de un círculo:
Ejemplo: obtener la medida del volumen de un cilindro cuya altura es de 35 cm y el radio de su base es de 9 cm.
Conos
La fórmula para calcular el volumen de un cono es: volumen es igual pi por radio al cuadrado por la altura entre tres.
O dicho de otra manera: volumen del cono es igual al área de la base por la altura entre tres.
Ejemplo: obtener la medida del volumen de un cono cuya altura es de 35 cm y el radio de su base es de 9 cm.
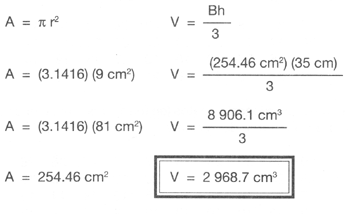
Ejercicios
1 El volumen de un cono es de 250 cm3. Calcula su altura si su radio mide 2.5 cm.
2 El volumen de un cilindro es de 1808.64 cm3 y el radio de su base es de 6 cm. Calcula su altura.
3 ¿Cuál es el volumen del siguiente cilindro si su altura es de 30cm y su radio de 12cm?
4 Con las mismas dimensiones del cilindro anterior, calcula el volumen de un cono incrustado dentro este cilindro.