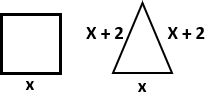Leyes de los Exponentes
Primera Ley: “Producto de potencias”
El producto (multiplicación) de potencias de la misma base, se calcula dejando la misma base y, como exponente, la suma de los exponentes.
Segunda Ley: “Cociente de potencias”
El cociente (división) de potencias de la misma base, se calcula dejando la misma base y como exponente la resta de sus exponentes. Al exponente del dividendo (arriba), se le resta el exponente del divisor (abajo).
Tercera Ley: “Potencia de potencias”
La potencia de otra potencia de la misma base, se calcula dejando la misma base y como exponente el producto (multiplicación) de los exponentes.
Ejercicios
1
2
3
4
Respuestas
Porcentajes
El porcentaje representa una parte de un total.
Para calcular un porcentaje A de un número B se aplica la fórmula:
Para encontrar el equivalente en porcentajes de un número con respecto a otro, utilizamos la regla de 3.
Ejercicios
1 En un grupo de secundaria hay 70 alumnos, 27 son hombres. ¿Cual es el porcentaje de mujeres en el salón?
2 De los 800 alumnos de un colegio, han ido de viaje 600. ¿Qué porcentaje de alumnos ha ido de viaje?
3 Un tanque de agua contiene 250 litros, lo cual representa un 18% de su capacidad total, ¿cuantos litros de agua le caben?
4 El precio de un teléfono es de $1200 sin IVA. ¿Cuánto hay que pagar por él si el IVA es del 16%?
Respuestas
Volumen de prismas
Un prisma es un cuerpo geométrico que está limitado por dos polígonos planos, paralelos e iguales, que se llaman bases; y por otros tantos paralelogramos, como número de lados tengan dichas bases.
El volumen de un prisma se obtiene multiplicando el área de la base por la altura del prisma.
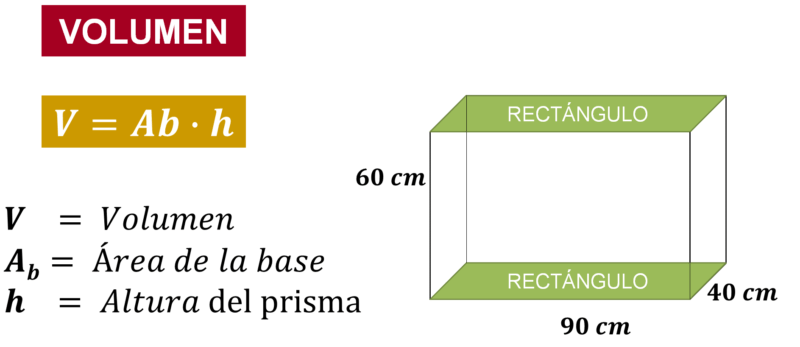
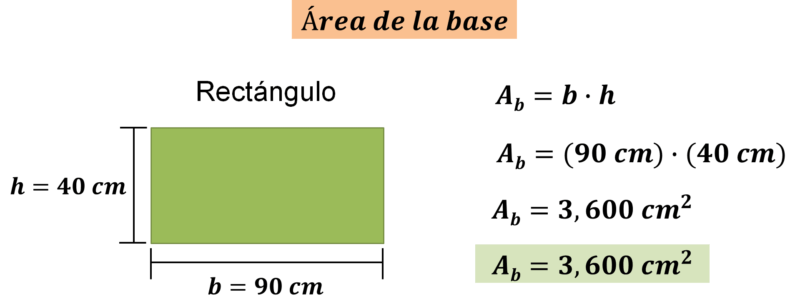
Para calcular el volumen del prisma de base rectangular, utiliza la fórmula antes mencionada, y para ello es necesario calcular, en primer lugar, el área de la base.
Una vez obtenida el área de la base, sustitúyela en la fórmula para calcular el volumen
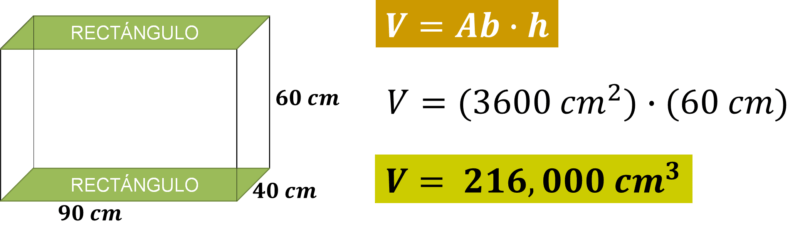
Ejercicios
1 Expresa el volumen del siguiente prisma:
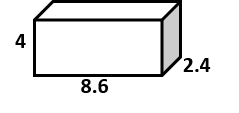
2 ¿Qué altura alcanza el agua en esta pecera, sabiendo que contiene 171 litros de agua?

3 Las dimensiones de una caja de naipes son de 3 x 2 x 0,5 pulgadas. Si las dimensiones de cada naipe son 3 x 2 x 0,01 pulgadas. ¿Cuántos naipes caben en la caja?
4 El costo de cavar una zanja es de $30 por metro cúbico. ¿Cuál es el costo de cavar otras cuyas dimensiones son 2m x 4,5 x 3m?
Respuestas
Ecuaciones Lineales (Sencillas)
Las ecuaciones lineales o de primer grado son del tipo ax+b=0, con a ≠ 0, ó cualquier otra ecuación en la que al
operar, trasponer términos y simplificar adopten esa expresión.
En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:
1 Quitamos los paréntesis
Esto es, si hay expresiones del estilo
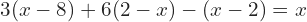
Entonces desarrollamos tomando en cuenta la propiedad distributiva y la ley de los signos.

2 Quitamos denominadores
En el caso que existan términos fraccionarios en la expresión, debemos identificar los diferentes denominadores
que haya, calcular el mínimo común múltiplo (mcm) de estos y multiplicar la ecuación por el mcm. O en vez
del mcm, también puedes calcular el producto de todos los denominadores aunque se recomienda más el primero,
pues es un número más pequeño o más simplificado. Por ejemplo:
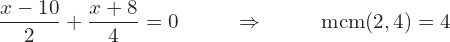
Multiplicamos todo por 4

Aquí de nuevo podríamos necesitar quitar paréntesis para simplificar

3 Agrupamos los términos en x en un lado y los términos independientes en el otro
Ya que hayamos hecho el paso 1 y el paso 2, tendremos la suma y resta de términos con x y términos independientes
de ambos lados de la ecuación, lo que sigue es juntar las x de un lado y los términos independientes del otro,
para esto recuerda que si de un lado de la ecuación se está sumando un 2x, por ejemplo, lo puedo pasar del otro
lado con la operación inversa, es decir, quedaría -2x del otro lado


4 Reducimos los términos semejantes
Ya que tengo los términos con x juntos, los sumamos o restamos dependiendo. De igual manera con los términos independientes, por ejemplo:

5 Despejamos la incógnita
Si hay un coeficiente acompañando a la variable x, como la está multiplicando lo pasaré del otro lado con la operación inversa,
esto es, dividiendo. A esto le llamamos despejar.
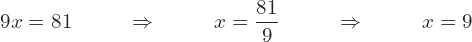
Ejercicios
1 Resuelve las siguiente ecuación:
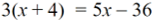
2 Encuentra el valor de X del siguiente rectángulo, si su perímetro es de 136 cm.

3 Sean A, B y C ángulo de un triángulo. Si B mide el doble de A y C el triple que B.
Hallar la medida del ángulo C.
4 Hallar el valor de X si el cuadrado y el triángulo siguientes tienen el mismo perímetro.